[中問C]
テストの採点結果の分析に関する次の記述を読んで、問に答えよ。
F教育機関では、P、Q、R、S、T、Uの六つの組がある。各組の受講生数は、P、Q組が35名、R組が25名、S、T、U組が30名である。このたび、6組共通のテストを行い、採点結果の分析を行うことになった。
[テストの採点結果の分析の概要]
(1)テストの問題数は10問で、1問を1点として、10点満点である。
(2)図1は、テストの採点結果入力のワークシートである。ワークシートのセルB2~B36には、P組の受講生の得点を入力する。同様に、ワークシートの列C~Gに、それぞれQ~U組の得点を入力する。
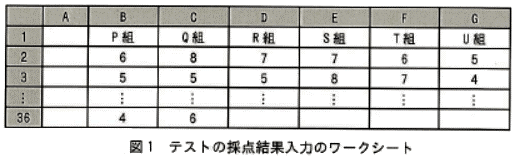
(3)テストの採点結果の分析は、得点の平均(以下、平均点という)及び標準偏差を使って行う。
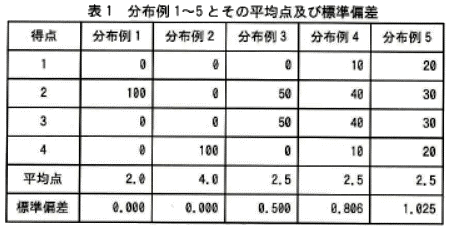
標準偏差は、得点のばらつきの度合いを表す指標である。受講生数がそれぞれ100人で、得点が1~4点に分布する表1の分布例1~5とその平均点及び標準偏差を例にとると、分布例1や分布例2のように、全員が同じ得点だった場合は、平均点に対して全く得点のばらつきがないことから標準偏差は0になる。また、分布例3~5のように、平均点が同じでも、得点のばらつきが大きいほど、標準偏差は大きくなる。
P~S組の平均点と標準偏差は、表2のとおりであった。この四つの組の中で、他の組に比べて成績が良くも悪くもなく、また、多くの受講生がその組の平均点に近い得点をとった組があった。その組では、得点が4~6点だった受講生の割合が他の組に比べて最も多かった。その組はどれか。

ア:P
イ:Q
ウ:R
エ:S
答:ウ
他の組に比べて成績が良くも悪くもなくという設問から、平均点が最高のP組と、平均点が最低のQ組は除外できる。
また、受講生の得点が4~6点に集中していると、得点のばらつきを示す標準偏差が小さくなる。
よって正解はウとなる。