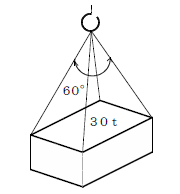
図のように質量30tの荷を、4本の玉掛け用ワイヤロープを用いてつり角度60°でつるとき、使用することができる最小径のワイヤロープは、次のうちどれか。
ただし、4本のワイヤロープには均等に荷重がかかるものとし、また、ワイヤロープの切断荷重は、それぞれに記載したとおりとする。
1:ワイヤロープの直径(mm)=28 切断荷重(kN)=359
2:ワイヤロープの直径(mm)=30 切断荷重(kN)=412
3:ワイヤロープの直径(mm)=32 切断荷重(kN)=469
4:ワイヤロープの直径(mm)=36 切断荷重(kN)=593
5:ワイヤロープの直径(mm)=40 切断荷重(kN)=732
答:4
ワイヤロープ1本に掛かる張力=質量÷つり本数×重力の加速度×張力係数
重力の加速度=9.8m/s2
つり角度60°の場合の張力係数=1.16
30t÷4本×9.8m/s2×1.16=85.26
玉掛け用ワイヤロープの安全係数は6以上必要である。
この場合に必要となるワイヤロープの切断加重=85.26×6=511.56
切断加重511.56以上で最小径のワイヤロープは36mmである。